Статистика игральных костей

05 жовтня 2015 р. 19:20

Вступление

В первую очередь представленные далее данные будут полезны ведущим, или дизайнерам систем, но и игрокам это тоже может быть полезно.

Разные системы настольных ролевых игр используют разные способы проверки успешности действий. Они различаются по равномерности распледеления вероятностей, по сложности "прикидывания" вероятности выбросить то или иное значение, ну и по самому способу подсчета результата:

В некоторых прикинуть шансы выпадения того или иного значения, а также среднее значение весьма просто (1d20 — в среднем 10.5, 1d100 — в среднем 50.5), но они при этом страдают черезчур сильным разбросом успешности/неуспешности проверок — вероятность выпадения минимума такая же как вероятность выпадения максимума
Другие чуть сложнее, зато позволяют рассчитывать на некоторую стабильность — вероятность выпадения средних значений больше чем минимальных и максимальных (сумма на 2d6, 3d6, Xd10), подсчёт точных вероятностей тут сложнее, но приблизительно прикинуть всё-равно несложно: среднее это просто (максимум+минимум)/2 (2d6 — 7, 3d6 — 10.5, Xd10 — 5.5*X, Xd6 — 3.5*X), а вероятность выпадения среднего растёт относительно вероятности выпадения крайних значений с каждым увеличением количества кубиков.
А есть системы которые относительно легко "бросать", но сложнее считать. Из простейших, например, популярный способ генерации статов в D&D — 4d6 с выбором 3х лучших вариантов (sum(4d6 keep 3) == sum(4d6k3)). Интуитивно понятно что он примерно такой же как 3d6, только в среднем даёт большие значения, но так сходу нельзя ответить ни на один из вопросов: какое среднее значение? насколько график "острее" в районе среднего значения (как поменялось значение среднеквадратичного отклонения)? Потом еще есть системы где надо считать не сумму на дайсах, а количество дайсов на которых выпало определённое значение (cWoW — количество кубиков где выпало >= сложности, при броске Xd10, count(Xd10, >=Target), или "усложнённые" варианты выбора лучших значений (DtD сумма Y лучших значений при броске Xd10, Xd10kY)
А ещё в некоторых системах есть "взрывы" кубиков, например в WoD и DtD когда на 1d10 выпадает 10 -- этот кубик учитывается в результат, но кидается ещё раз.

Прежде чем предоставить статистику, нужно затронуть немного теории.

Теория

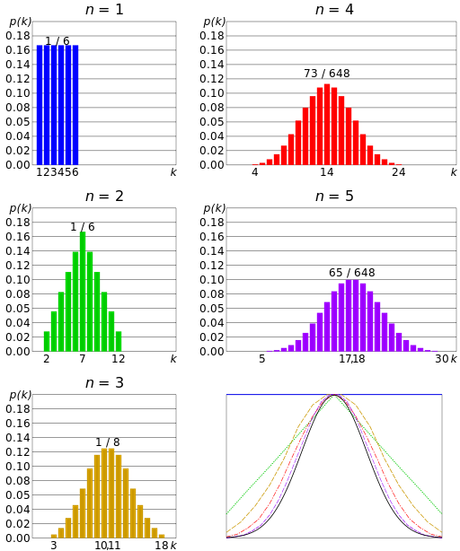
Начнём с плотности вероятности случайной величины. Грубо говоря, график на котором видно вероятность выпадения того или иного значения это график плотности вероятности. Вот графики (с вики) вероятности получить различные суммы на одном, двух, трёх, четырёх и пяти кубиках (графики из википедии):

На последнем графике они сравниваются с нормальным распределением (черная линия). На нём видно, что чем больше кубиков, тем больше график соответствует нормальному распределению. И так:

Математическое ожидание (μ) в нормальном распределении, это координата x его "центра", т.е. среднее значение выпадающей величины.

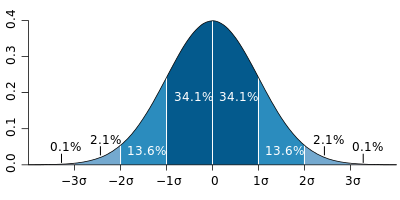
Среднеквадратическое отклонение (σ) — показатель "размазанности" распределения. Вероятность того, что случайная величина будет в пределах - μ-σ.. μ+σ примерно равен 68%, т.е. большая чать всех случайных значений будет в этих пределах. А в пределах μ-2σ.. μ+2σ будет уже 95% все. Зачем это знать? Ну если вызнаете сколько вам нужно выкинуть на кубиках, то зная в какой из диапазонов попадает величина можно представить себе вероятность попадания без запоминания всего графика: μ..μ+σ — 34%, μ+σ..μ+2σ — 14%.

График из википедии:

Стоит заметить что для распределений отличных от нормального эти проценты будут другие, но всё-же если распределение похоже, то значения будут приблизительно похожи.

Пример для 4d6k3

Рассмотрим, например sum(4d6k3):

Математическое ожидание: 12.2, т.е. усреднённое значение всех бросков близко к 12, но несмотря на это чаще всего выпадает 13 (распределение не симметричное)
среднеквадратичное отклонение: 2.8, т.е. значения с 12.2 по 12.2+2.8 (т.е. реально 13,14,15) выпадают с вероятностью примерно 34%. Однако это распределение отличается от Гауссового, и в реальности вероятность выпадения этих значений будет 13%+12%+10% =35%, что не сильно отличается от нормального распределения
В общем случае вероятность выпадения значений в определённом диапазоне можно посчитать просто суммируя вероятности каждого из этих значений. Например: вероятность выкинуть 9 или меньше: (0.08+0.31+0.77+1.6+2.9+4+7)% ≈ 17%

Графики плотности вероятностей для sum(2d6), sum(3d6), sum(3d6k3), 1d6! (со взрывами):

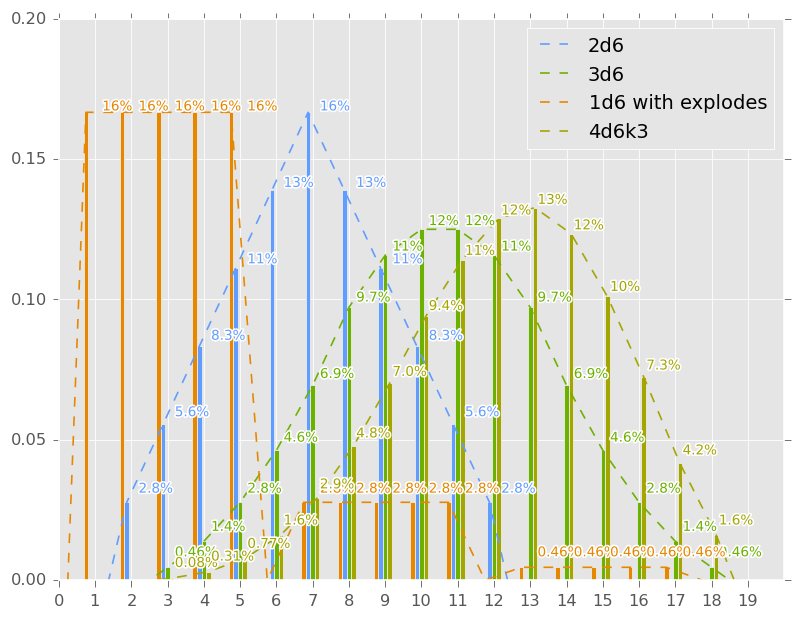
Различные системы

Dungeons & Dragons

Большинство проверок сводится к "выбросить на 1d20 больше чем DC-skill" или к аналогичным. Для данной простой проверки даже графики-то не нужны, всё можно посчитать в уме. Вероятность выкинуть 10 или больше: 1/20*11 = 55%. Вероятность выкинуть 15 или больше: 6/20 = 30%

немного сложнее с новой системой Advantage/Disadvantage, когда бросается 2d20, и берется лучшее/худшее значение: min(2d20) и max(2d20). Вот графики для них:

При наличии advantage вероятность выбросить 20 — почти 10%! Аналогичная вероятность выкинуть 1 при disadvantage. Плотности вероятности обоих вариантов являются зеркальными отображениями друг-друга, поэтому свойства одной "зеркально" являются свойствами другой.
Математическое ожидание смещается на 3.3 вправо или влево. Однако распределение не Гауссово, и даже не похоже на изначальное, так-что это не эквивалентно бонусу/штрафу 3.3
при advantage вероятность получить 9 или меньше 20%, в то время как на обычном 1d20 —45%

Броски 2dN с выбором лучшего/худшего хороши для процессов вида "чем больше, тем вероятнее" или "чем меньше тем вероятнее", например при случайном выборе "силы" для воина, или при выборе количества трезвенников в баре, количество проституток в церкви, количество честных людей в правительстве, средняя школьная оценка мелкого воришки, вероятность что кошка приземлится на ноги. Так же эти броски хороши для описания процессов которые следуют закону Мерфи, например вероятность что бутерброд упадёт маслом вниз.

Хоббиты

Везучие хоббиты могут перекидывать кубик, если на нём выпало значение 1. Если вам интересно как это влияет на вероятности выбросить то или иное значение, то можете изучить следующие графики

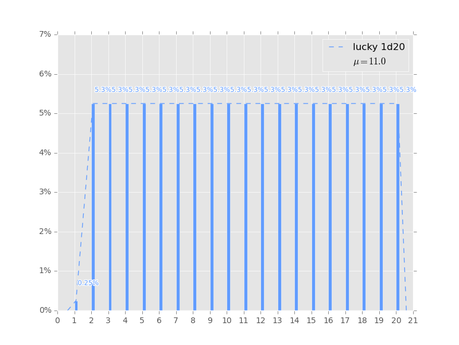
Тут всё просто: вероятность получить 1 — 1/5

При наличии преимущества, вероятность получить 1 у халфлинга меньше одной тысячной процента, а остальное видно на графике

New World of Darkness

в WoD кидается Xd10, и считается количество костей на которых выпало 8 или больше. Кости на которых выпало 10 учитываются в успех и кидаются ещё раз, и учитываются так же как и первые брошенные кости, если опять выпадает 10, то процесс повторяется. Т.е. возможно да же на 1d10 выкинуть бесконечное значение успехов, правда вероятность этого очень низкая. Как оказалось, график плотностей вероятности данного вида бросков лучше всего отображается используя логарифмическую шкалу. Для тех кто не знает: на логарифмической шкале одно деление означает увеличение/уменьшение значения в 10 раз, на два деления — в 100 раз и т.д.

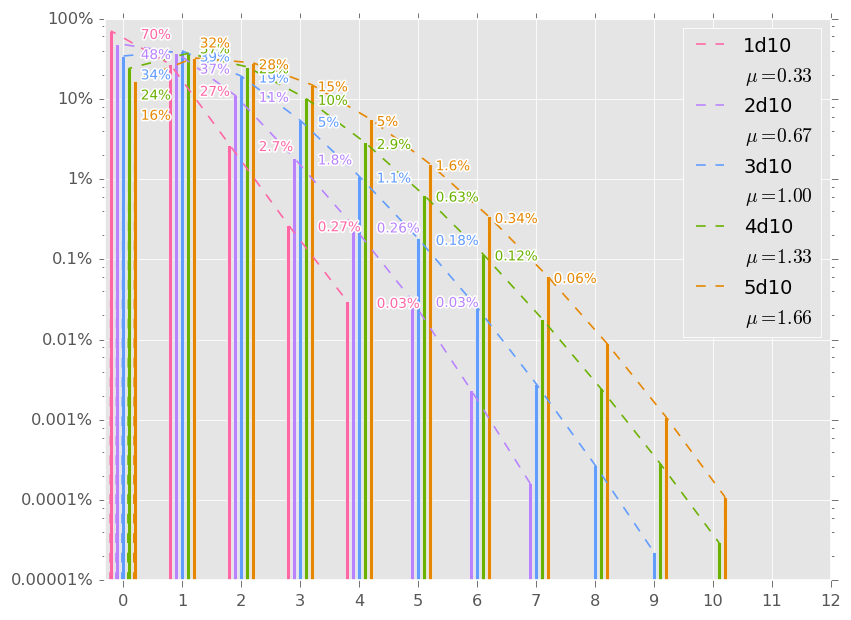
По графику видно что при такой системе подсчёта результатов при броске Xd10 вероятности 0..(X-1) успеха достаточно велики. Вероятность выпадения X и больше падает во много раз с каждым новым успехом.

Такие броски хорошо описывают процессы где вероятность определённых значений отличаются не сильно, но уменьшается с ростом величины. При этом несмотря на наличие границы, есть очень маленькая вероятность получить и большие значения. Такое распределение неплохо подходит для событий имеющих какие-то ограничения, которые при этом всё же изредка могут быть преодолены

Dungeons the Dragoning

В DtD, как и в WoD бросается Xd10 со "взрывами" кубиков и выбором N лучших значений, а вместо "количества по условию" считается сумма. Далее представлены графики для Xd10, графики для Xd10kN не отображены, но по аналогии с 4d6k3 они будут похожи на ND10 со сдвигом медианы (верхушки) правее с каждым X.

Данный вариант является компромиссным между "колоколовидным" распределением, где чаще всего выпадает определенное значение, и есть меньшая вероятность выпадения малых/больших значений , и распределением как в nWoD, когда нет верхнего предела значений, но их вероятность очень мала. Правда тут все же высокие значения выпадают чаще чем в nWoD, так-что на 3d10 где в среднем выпадает 15-16, вполне можно получить и 50 за одну игровую сессию несколько раз

Итоги

Разные способы подсчета результата лучше всего описывают события или действия разной природы. С событиями всё просто — их природа видна по графикам. А вот с действиями чуть сложнее — разные системы описывают разную степень влияния персонажа (модификатора) на результат: где-то все больше зависит от персонажа, где-то больше от случая.

1dN+mod >= target, если порядок mod примерно такой же как и N, например 1d20+3, 1d20+10. Описывает действия, эффективность которых мало зависит от персонажа, а модификатор просто немного увеличивает эффективность
1dN+mod >= target, если mod в разы больше N, например 1d6+20, 1d20+50. Описывает действия эффективность которых более менее стабильна, но может колебаться в окрестностях mod+((N+1)/2)
max(2dN)+mod >= target. Описывает действия эффективность которых в основном зависит от персонажа (mod), и как правило они максимально эффективны, но есть факторы которые могут уменьшить эффективность.
max(3dN)+mod >= target. Тоже самое что и max(2dN), но с еще большей вероятностью получить максимальное значение
sum(XdN)+mod >= target, когда X>=2. Описывает действия эффективность которых, как правило, напрямую зависит от персонажа, но есть факторы которые могут увеличить или уменьшить эффективность.
count((mod)dN >= constant value) >= target. Описывает действия где диапазон эффективностей напрямую зависит от персонажа. Сама эффективность тоже зависит от персонажа, но в меньшей степени. Эффективность больше диапазона очень мало-вероятна, но возможна
sum((mod)dN) >= target. Описывает действия где от персонаж зависит и эффективность, и "стабильность" эффективности и диапазон эффективности. Эффективность больше диапазона вероятна и ничем не ограничена, но маловероятна (но более вероятна чем для count((mod)dN >= constant value) >= target)
Вариации XdN keep Y best, где X>=2, 2 <=Y<=X. Аналогичны YdN, но увеличение X увеличивает вероятность большей эффективности и сильно уменьшает вероятность минимальной эффективности. Например в DtD: (mod1)d10k(mod2): mod2 определяет диапазон, эффективности и стабильность эффективности, mod1 — увеличивает стабильность и вероятность "сверх-эффективности"

Если вам хочется самим построить подобные графики и вы умеете программировать на python, то можете скопировать мой репозиторий и что-нибудь поменять

автор: Ярослав Клюев (imposeren)